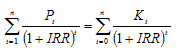Vnútorné výnosové percento je dynamická metóda, kde IRR je taká úroková miera, pri ktorej sa súčasná hodnota peňažných príjmov rovná (súčasnej hodnote) kapitálových výdavkov.
Ak IRR je vyššie ako požadovaná minimálna výnosnosť projektu (i), projekt je prijateľný.
Ak IRR je nižšie ako požadovaná minimálna výnosnosť projektu (i), projekt je neprijateľný.
Pri porovnaní dvoch projektov stále vyberáme projekt s vyšším vnútorným výnosovým percentom.
NPV a IRR sú založené na iných predpokladoch, čo sa týka reinvestovania príjmov:
- NPV použijeme, ak peňažné príjmy reinvestujeme za použitú úrokovú sadzbu i
- IRR použijeme, ak peňažné príjmy reinvestujeme za IRR (čo je nereálne).
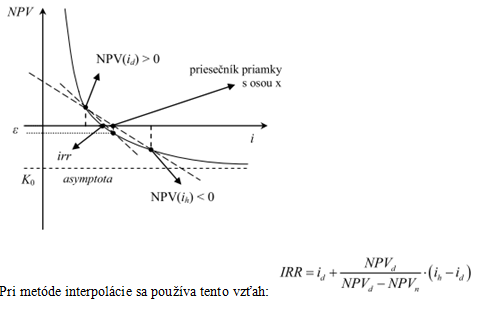
Grafické znázornenie hľadania IRR iteračnými postupmi (ak máme funkciu 5. a vyššieho rádu):
, kde id je nižšia i (dolná i) ; ih je vyššia i (horná i).
Funkcie vyššieho ako 5. rádu nevieme riešiť, IRR iba odhadujeme. Pôjdeme metódou pokus-omyl. Zvolíme si také dve i, aby NPV1 > 0 a NPV2 < 0. Medzi týmito hodnotami leží hodnota IRR. Mám 2 body, cez ktoré preložím priamku a vyjadrím jej rovnicu (y = k . x + q). Vypočítam jej funkčnú hodnotu s priesečníkom osi x, dostanem odhadované IRR (označme ho ako ip). Na začiatku si stanovím, že odchýlka medzi priesečníkom priamky s osou x (ip)a funkčnou hodnotou NPV pri tejto hodnote bude ε (konkrétna hodnota, napr. 0,01). Získanú ip dosadím do funkcie NPV, a ak táto hodnota bude menšia ako ε, končím s výpočtom a s požadovanou presnosťou môžem povedať, že ip = IRR. Ak nie, tak hodnotu získanú hodnotu NPV považujem za nový bod a postup opakujem.
Príklad:
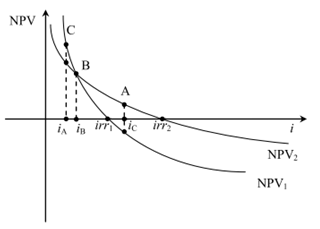
Ak vychádzame z obrázka, vyberáme z dvoch projektov, Projekt 1 a Projekt 2, ktorý projekt je na základe NPV a IRR výhodnejší?
Riešenie príkladu:
Ak sa pozrieme na situácia A, máme alternatívnu úrokovú sadzbu iC. Ak sa na tieto projekty pozrieme z hľadiska NPV, zvolíme Projekt 2, pretože ako jediný má NPV kladný. Zároveň, ak sa na situáciu pozrieme z pohľadu IRR, výhodnejší je Projekt 2, pretože IRR2 > IRR1.
Ak sa pozrieme na situáciu B, máme alternatívnu úrokovú sadzbu iB. Ak sa na tieto projekty pozrieme z hľadiska NPV, nevieme sa rozhodnúť, pretože obe projekty majú rovnakú hodnotu NPV. Musíme sa rozhodnúť na základe IRR. Vyberáme Projekt 2, pretože IRR2 > IRR1.
Ak sa pozrieme na situáciu C a posudzujeme projekty na základe NPV, výhodnejší je Projekt 1, pretože pri alternatívnej úrokovej sadzbe iA má vyššiu hodnotu NPV. Ale, ak sa na to pozrieme z hľadiska irr, irr2 > irr1, znamená to, že podľa IRR by sme mali vybrať projekt 2. Pri tejto situácii sa rozhodujeme na základe NPV.